Fractional ideal

In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed. In contexts where fractional ideals and ordinary ring ideals are both under discussion, the latter are sometimes termed integral ideals for clarity.

1 Definition and basic results
2 Dedekind domains
3 Other notions
4 Notes
5 References

Definition and basic results

Let R be an integral domain, and let K be its field of fractions. A fractional ideal of R is an R-submodule I of K such that there exists a non-zero r ∈ R such that rI ⊆ R. The element r can be thought of as clearing out the denominators in I. The principal fractional ideals are those R-submodules of K generated by a single nonzero element of K. A fractional ideal I is contained in R if, and only if, it is an ('integral') ideal of R.

A fractional ideal I is called invertible if there is another fractional ideal J such that IJ = R (where IJ = { a₁b₁ + a₂b₂ + ... + a_nb_n : a_i ∈ I, b_i ∈ J, n ∈ Z_>0 } is called the product of the two fractional ideals). The set of invertible fractional ideals form an abelian group with respect to above product, where the identity is the unit ideal R itself. This group is called the group of fractional ideals of R. The principal fractional ideals form a subgroup. A (nonzero) fractional ideal is invertible if, and only if, it is projective as an R-module.

Every finitely generated R-submodule of K is a fractional ideal and if R is noetherian these are all the fractional ideals of R.

Dedekind domains

In Dedekind domains, the situation is much nicer. In particular, every non-zero fractional ideal is invertible. In fact, this property characterizes Dedekind domains: an integral domain is a Dedekind domain if, and only if, every non-zero fractional ideal is invertible.

The quotient group of fractional ideals by the subgroup of principal fractional ideals is an important invariant of a Dedekind domain called the ideal class group. Part of the reason for introducing fractional ideals is to realize the ideal class group as an actual quotient group, rather than with the ad hoc multiplication of equivalence classes of ideals.

Other notions

Let 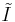$\tilde I$ denote the intersection of all principal fractional ideals containing I. Equivalently,

$\tilde I = (R�: (R�: I)),$

where

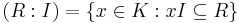$(R�: I) = \{ x \in K�: xI \subseteq R \}$ .

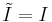If $\tilde I = I$ then I is called divisorial.^[1]

Notes

^ Bourbaki 1998, §VII.1

References

Chapter 9 of Atiyah, Michael Francis; Macdonald, I.G. (1994), Introduction to Commutative Algebra, Westview Press, ISBN 978-0-201-40751-8
Chapter VII.1 of Bourbaki, Nicolas (1998), Commutative algebra (2nd ed.), Springer Verlag, ISBN 3-540-64239-0
Chapter 11 of Matsumura, Hideyuki (1989), Commutative ring theory, Cambridge Studies in Advanced Mathematics, 8 (2nd ed.), Cambridge University Press, ISBN 978-0-521-36764-6, MR 1011461